The spring rate shows how much force a spring needs to stretch or squeeze by a certain distance. To calculate spring rate for tension springs, this measurement indicates how well the spring can handle weight without breaking. You can find the spring rate using this formula:
Rate = (Load - Initial Tension) / Travel
This formula is important in engineering because it helps springs work properly. For example, changing a weight of 0.75 pounds to 3.336 Newtons and a movement of 0.05 inches to 1.27 millimeters allows you to calculate spring rate, resulting in a value of 15 pounds per inch. Correct calculations stop springs from breaking and make them last longer, which is crucial for design and use.
Key Takeaways
Learn the spring rate formula: Rate = (Load – Initial Tension) / Travel. This shows how much force the spring can handle.
Pick the right wire thickness. Thicker wires are stronger and stiffer. Thinner wires bend more easily. Choose based on what your spring needs.
Think about coil size and number of active coils. Bigger coils make softer springs. More active coils let the spring move more. Change these to fit your design.
Choose the right materials. Different materials work differently in springs. Match the material to how the spring will be used.
Always include preload in your math. Preload changes how much force is needed to stretch the spring. This helps it work correctly.
Key Factors for Calculating Spring Rate
Knowing the main factors that affect spring rate helps in designing tension springs. Each factor changes how the spring works when weight is applied.
Wire thickness and its importance
The thickness of the wire changes the spring’s strength and stiffness. Thicker wires make springs stronger and able to hold more weight. Thinner wires are more flexible but can’t handle as much force.
Tip: Check how stress spreads across the wire. Picking the right thickness makes springs last longer and work better.
Strength and Stiffness: Thicker wires make springs stiffer and stronger.
Flexibility: Thinner wires bend more but are less strong.
Stress Spread: Wire thickness affects how long the spring will last.
Average coil size and why it matters
The average size of the coils decides the spring’s size and energy storage. Measure the middle size of the coils to find this. Bigger coils make softer springs, while smaller coils make stiffer ones.
Note: Exact coil size is key for things like race cars. Formula One cars need perfect spring rates to improve tire grip and speed during races.
Active coil count
The number of active coils changes the spring’s stiffness. More coils make springs softer and allow more movement. Fewer coils make springs stiffer and harder to bend.
Active Coil Count | Effect on Spring Stiffness |
|---|---|
More Coils | Softer spring with more movement |
Fewer Coils | Stiffer spring with less movement |
When figuring out spring rate, think about how many coils fit your design. Add coils for softer springs. Remove coils for stiffer ones.
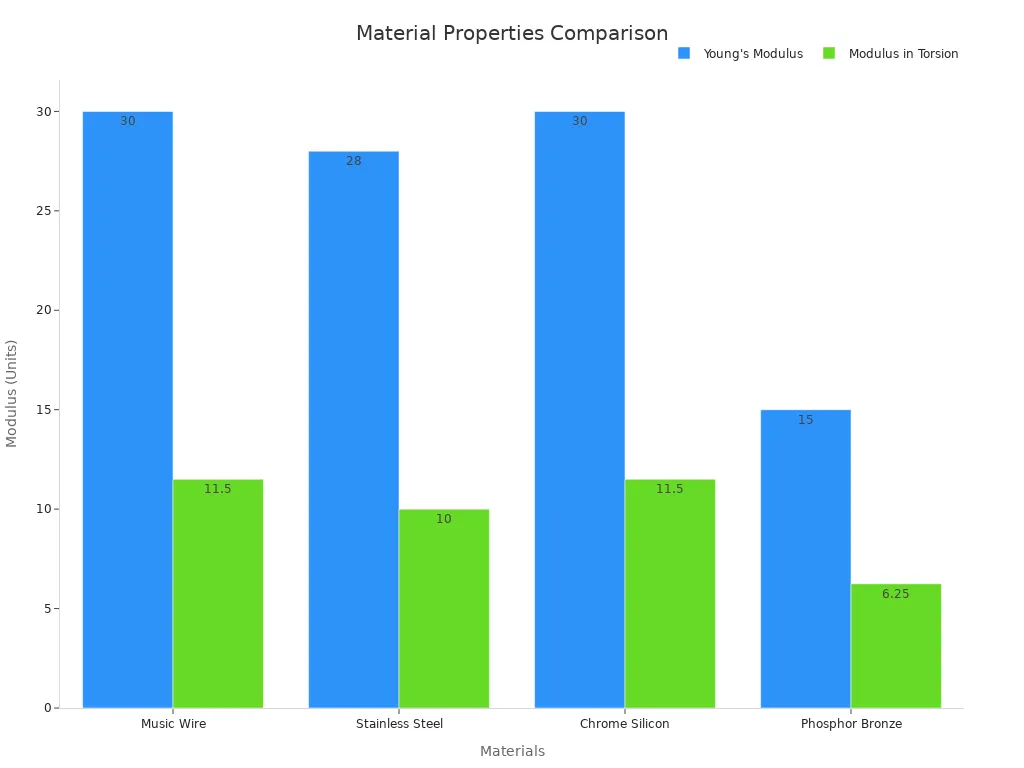
Material properties and modulus of rigidity
The material of a tension spring affects how it works. Different materials have special traits like Young’s modulus (E) and modulus in torsion (G). Young’s modulus shows how stiff the material is. Modulus in torsion measures how well it resists twisting. These traits decide how much energy the spring can store and if it returns to its shape.
Here’s a table comparing common spring materials:
Material | Young’s Modulus (E) | Modulus in Torsion (G) |
|---|---|---|
Music Wire | 30 | 11.5 |
Stainless Steel | 28 | 10 |
Chrome Silicon | 30 | 11.5 |
Phosphor Bronze | 15 | 6.25 |
For example, music wire and chrome silicon are stiffer and resist twisting better. They are great for heavy-duty jobs. Phosphor bronze is softer and good for light loads or places with rust risks.
Tip: Pick a material that matches your spring’s job. This helps it work well and last longer.
Preload and its impact on calculations
Preload is the tension in a spring before adding any force. It keeps the spring tight and ready to work. Preload changes how much force is needed to stretch the spring more.
For example, take a spring that is 14 inches long, with a spring rate of 600 lbs, and a preload of 1 inch. The preload shortens the spring’s working length to 13 inches, as shown here:
Spring Length | Spring Rate | Preload Applied | Resulting Compression |
|---|---|---|---|
14 inches | 600 lbs | 1 inch | 13 inches |
Preload stops the spring from being loose or moving too much. But it also changes the force needed for extra stretching. Always include preload in your spring calculations.
Note: Measure preload carefully and add it to your math. This avoids mistakes and ensures the spring works right.
Formula to Calculate Spring Rate
Understanding the formula parts
To find the spring rate, you must know the formula’s parts. Each part helps explain how a tension spring works under weight. The formula is:
Rate = (Load - Initial Tension) / Travel
Here’s what each part means:
Load: The weight or force on the spring, in pounds or newtons.
Initial Tension: The built-in force in the spring before adding weight.
Travel: How far the spring stretches or compresses, in inches or millimeters.
Check this table for related terms and formulas:
Component | Formula/Definition |
|---|---|
Mean Diameter (D) | D = D outer – d |
Shear Modulus (G) | G = E ÷ 2 (1 + V) |
Spring Rate (k) | k = Gd^4 ÷ (8D^3 * n) |
Hooke’s Law | k = F ÷ x |
Wire Diameter (d) | Thickness of the spring wire |
Outer Diameter | The spring’s total outside diameter |
Young’s Modulus (E) | Measures how stiff the material is |
Poisson’s Ratio (v) | Compares sideways stretch to length stretch |
Active Coils (n) | Coils that affect the spring’s strength |
Knowing these parts helps you calculate correctly and design springs that work well.
Why units of measurement matter
Using the right units is key when finding the spring rate. It keeps your math correct and avoids mistakes. Both imperial and metric units are used, depending on the job.
Measurement Type | Imperial Units | Metric Units |
|---|---|---|
Load | Pounds (lbs) | Newtons (N) |
Distance Traveled | Inches (in) | Millimeters (mm) |
Spring Rate | Pounds per inch (lbs/in) | Newtons per millimeter (N/mm) |
Torsion Spring Rate | Inch-pounds per degree (in-lbs/deg) | Millimeter-Newtons per degree (mm-N/deg) |
For example:
Car suspensions often use pounds per inch because of U.S. standards.
Machines in factories use metric units like newtons per millimeter for global use.
Always switch between units carefully to keep your math accurate.
Hooke’s Law and how it works for tension springs
Hooke’s Law explains how tension springs behave. It says the force a spring gives matches how much it stretches, as long as it doesn’t stretch too far. The formula is:
F = kx
Where:
F is the force on the spring.
k is the spring rate.
x is how much the spring stretches or compresses.
Tests prove Hooke’s Law works for tension springs. Scientists measured force and stretch, then graphed the results. The graph showed a straight line until the spring stretched too much. This means Hooke’s Law is reliable if the spring stays within its limits.
When designing springs, use Hooke’s Law to figure out the force needed for a certain stretch. This helps you pick the right spring and ensures it works properly.
Step-by-Step Calculation Process
Example 1: Finding spring rate for a basic tension spring
Follow these steps to find the spring rate:
Find Mean Diameter (D): Take the outer diameter (OD) and subtract the wire diameter (d).
Formula:D = OD − dFind Spring Rate (k): Use this formula:
k = Gd^4 ÷ (8D^3 * n). Here, G is the modulus of rigidity, d is the wire thickness, D is the mean diameter, and n is the number of active coils.Insert the values: Put the numbers into the formula to calculate the spring rate.
For example, use these details:
Parameter | Example 1 |
|---|---|
C | |
G | 80400 |
d | 2 mm |
Dm | 10 mm |
Nw | 8 |
With these numbers, you can find the spring rate correctly.
Example 2: Changing calculations for preload
Preload adds tension to the spring before use. To adjust for preload:
Find the preload force.
Subtract the preload from the total load before dividing by travel.
Use this updated load in the formula:
Rate = (Load - Preload - Initial Tension) / Travel.
For example, if a spring has a preload of 5 N and a total load of 20 N, the adjusted load is 15 N. This ensures your results are correct.
Mistakes to avoid when calculating
Watch out for these common errors:
Mistake | Description |
|---|---|
Stress Concentrations | Not checking stress at coil ends can give wrong results. |
Material Selection | Picking weak materials can make the spring fail. |
Design Parameters | Ignoring movement needs can make springs work poorly. |
Always double-check your math and material choices to avoid these problems.
Preload and Its Effect on Spring Rate
What is preload in tension springs?
Preload is the starting force on a tension spring. It keeps the spring tight and ready to work. Without preload, the spring might be loose and not work well. Preload stops the spring from moving until enough force is added.
For example, if a spring has a preload of 55.66 Newtons and a spring rate of 54.12 Newtons per millimeter, stretching it by 3 millimeters needs 218.02 Newtons. This includes the preload, making sure the spring works properly.
How preload changes spring rate math
Preload changes how you calculate the spring rate. It affects the total force needed to stretch the spring. To adjust for preload, subtract it from the total force. This gives accurate results.
Look at this example:
Preload Effect | A | B | C |
|---|---|---|---|
Force Needed | 850 | 850 | 850 |
Preload | 50 | 75 | 100 |
Spring Stretch Needed | 50 | 50 | 50 |
N/mm | 16 | 15.5 | 15 |
In this table, preload changes the spring’s stretch and stiffness. Adding preload to your math ensures the spring works as planned.
Tips for handling preload in designs
When designing springs, think about preload carefully. Here are some tips:
Decide preload early: Figure out how much starting force is needed.
Try different preload levels: Test to find the best mix of stiffness and flexibility.
Include preload in math: Always add preload to avoid mistakes.
By managing preload well, you can create springs that work perfectly for your needs.
Practical Uses of Spring Rate Calculations
Picking the right tension spring with spring rate
Spring rate helps you choose the best tension spring. It shows how the spring reacts to weight or force. A high spring rate means the spring is stiff and needs more force to stretch. A low spring rate means the spring is flexible and needs less force to move. This lets you pick springs for specific jobs. For example, light tasks need flexible springs for smooth use. Heavy tasks need stiff springs to handle the weight well.
Tip: Always measure spring rate carefully to match it with your design.
Making tension springs for special uses
Creating tension springs for industries needs careful planning. Engineers adjust spring features for different jobs. For example, in cars, springs are made for electric vehicles to balance strength and flexibility in suspensions. In medical tools, springs are designed with exact spring rates for steady performance. For heavy machines like excavators, springs are redesigned to improve control and last longer.
Industry | Purpose |
|---|---|
Automotive Industry | Springs for electric cars, balancing strength and flexibility in suspensions. |
Medical Equipment | Springs for surgical tools, ensuring steady performance with precise spring rate designs. |
Heavy Machinery | Stronger excavator springs for better control and durability. |
Solving problems in spring rate calculations
Finding spring rate can be tricky, especially with complex designs or changing weights. One problem is dealing with preload, which changes how the spring works under force. Another issue is picking the right material, as each material affects the spring differently. To fix these problems, test springs in real conditions and adjust designs as needed. Using advanced software can also help you plan and improve spring behavior before making them.
Note: Solving these problems early ensures your tension springs work well for their jobs.
Knowing how to find spring rate is important for making good tension springs. The main formulas and steps make it easier. For example:
Formula | What It Does |
|---|---|
D = D outer – d | Finds the spring’s middle diameter. |
G = E ÷ 2 (1 + V) | Figures out the material’s shear modulus. |
Calculates spring rate using size and shape. | |
k = F ÷ x | Uses Hooke’s Law to get spring rate directly. |
Preload is very important for how a spring works. It keeps the spring ready to use with starting tension. For example:
Detail | Amount |
|---|---|
Preload Force | |
Spring Rate | 54.12 Newtons/mm |
Total Stretch Force | 218.02 Newtons |
Learning these ideas helps you make springs for specific jobs. Use this knowledge to build strong and useful springs for real-life needs.
FAQ
What is the difference between spring rate and stiffness?
Spring rate shows how much force stretches or compresses a spring. Stiffness means how hard it is to change the spring’s shape. Spring rate is a specific number, while stiffness is a general feature.
Why is preload important in tension springs?
Preload keeps the spring tight and ready to work. It stops extra movement and makes the spring perform better. Without preload, the spring might not work well, especially in precise tasks.
How do you convert spring rate units?
To switch spring rate units, use these steps:
From pounds per inch (lbs/in) to Newtons per millimeter (N/mm): Multiply by 0.1751.
From Newtons per millimeter (N/mm) to pounds per inch (lbs/in): Multiply by 5.71.
Tip: Always check your conversions to avoid mistakes.
Can you use Hooke’s Law for all springs?
Hooke’s Law works only if the spring stays within its limit. If stretched too far, the spring might not return to its shape. Always use springs within their safe range.
What happens if you miscalculate the spring rate?
Wrong spring rate math can cause bad performance or break the spring. For example, the spring might not hold the load or stretch right. Always double-check your math to avoid problems.